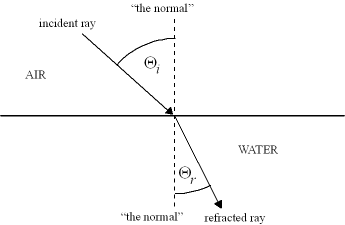
Snell's WindowYou may or may not have seen the effect before, but it's there, over your head, every time you dive. Look at the surface, and you'll probably see it: Snell's Window. It manifests itself as a bright circle directly overhead, while all the water outside the circle is darker. But there's another effect, one you'll see most when the surface water is calm: inside the circle, you can see objects on the surface clearly. Outside the circle, you can't. So why does Snell's Window exist, and exactly how big is it? Let's start with the equation that governs the bending (or "refraction") of light when it passes from one medium to another. Look at the diagram below, which shows a light beam going from air into water. When doing optics calculations, the convention is to measure angles from the "normal,"an imaginary line perpendicular to the surface in question. In the diagram, you'll see the line between the light beam and the normal in air marked as Qi ("i" is for "incident"), and the same thing on the water side as Qr ("r" is for "refracted"). There is one other piece of information we need: the index of refraction of both air and water. The index of refraction basically measures how much the medium in question bends light. To be precise, it's the ratio of the speed of light in that medium to the speed of light in a vacuum, but that's not important for this discussion. Suffice it to say that denser materials have higher index of refraction numbers. The equation we want is called "Snell's Law," after the mathematician who discovered the law in the 17th century.Snell's Law will let us explain and quantify Snell's Window, which is why the effect is named after the same person as the law. Anyway, here is a sketch that shows the geometries.
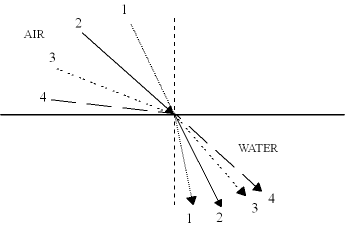
Using the geometries above, here is Snell's Law: ni Sin Qi = nr Sin Qr Remember, n is the index of refraction, and Q is the angle measured from the normal. So how does this help us explain Snell's Window? Let's start by making a few observations. First off, if a ray of light hits with zero angle (that is, perfectly perpendicular to the water), it will pass through with no bending. However, if it hits with some angle, the water will bend the light towards the normal. That is, for whatever angle it hits with, after it passes into the water the light will be closer to the normal than it had been. So if a ray of light hits at 30 degrees from vertical, it will end up in the water at a smaller angle, maybe 20 degrees from the vertical. This is an important observation. Why? Because the largest angle light can hit the water with is 90 degrees; at that point, it's not hitting the water, but rather is parallelling it. So if we plug 90 degrees into Snell's Law above, we can solve for the maximum angle from the vertical that light can ever have underwater! Think about that: at an incident angle of 90 degrees from the normal, light will still be bent towards the normal by the water, so it will enter the water at an angle less than 90 degrees! Here's the implication of that last statement:no direct light will enter your eyes at an angle larger than this. That's not to say that you don't get any light from greater angles, just that any light from greater angles must be scattering rather than refracting. It won't come in the form of an image you can see, but as a random and diffuse glow. Here's a sketch showing what happens:
You have to pay close attention to this sketch to understand it. Each ray of light is numbered, on both the air and water sides. Incident ray #1 becomes refracted ray #1, #2 becomes #2, etc. Notice how ray #1 is close to the normal, and stays close to the normal. As the incident rays get farther from the normal, so do the refracted rays--but the refracted rays get farther away "slower" than the incident rays do. Notice how ray #4, which strikes the water at an almost grazing angle in air, does not end up at anything like a grazing angle under water! So let's do some algebra, and get a number. We want to solve Snell's Law for Qr. We are also interested in the special case of light that just grazes the surface of the water, so plug90 degrees in for Qi. Then divide both sides by nr. Also note than Sin(90) = 1, so the Sin Qi factor goes away. Then our equation is: Sin Qr = ni / nr Now we solve for Qr by taking the inverse sine of both sides: Qr = sin-1 (ni/nr). For practical purposes, the index of refraction of air is 1.0, and the index of refraction of water is 1.33. Then we get Qr = sin-1 (1/1.33) = sin-1 (0.75) = 48.6 deg ~ 50 deg. So the magic angle is around 50 degrees. Since that's measured from the vertical, it means you get a cone of vision roughly 100 degrees wide over your head. There are two things worth noting here. (1) Light will never actually strike at an incident angle of 90 degrees, because it will reflect off the surface first. Thus the 48.6 degrees we arrived at earlier is probably more like 45 or even 42 degrees. Also, wave action at the surface will tend to 'smear' the actual incident angle, so there will be a fringe area close to the edges of Snell's window where some light makes it through and some doesn't. You can see this in pictures with Snell's Window in them; just look near the edges of the Window, and you will see patterns of light and dark that come from the waves. (2) Snell's Window has a corresponding inverse effect for light travelling from water into air (or from an medium with high index of refraction to one with low index). Just think about what would happen if the incident light ray were from the water at the 48.6 degree angle we derived above: it would "exit" the water at 90 degrees--that is, it would end up parallel to the surface of the water. At higher angles, it would actually reflect back into the water. This effect, known as "total internal reflection," is what makes fiber optic cables work. |
About | UW Photos | Scuba Picture Uv the Day | Flower Gardens | Aquashot | Trip Reports | RSDiver | Photo Instruction | News | Desktop/Screensaver Images | Site Map |
||